Batch 3 - Class 242 - Logic, Venn Diagrams
(zoom)
Pre-Class Exercise
- (Waterloo - Problem 11) There is a secret hall at Hogwart’s with magical closets. When you open a closet door, you might find Harry Potter, or you might find Voldemort. Since Hogwarts is magic, it is possible that both doors contain Harry Potter, or both doors contain Voldemort.
- (a) When you enter the secret hall, you encounter two closet doors. “One of the signs is true,” says Professor Snape,“and the other is false.”
- i. First Door: Harry is behind this door. Voldemort is behind the other.
- ii. Second Door: Harry is behind one of these doors. Voldemort is behind the other.
- Who is behind each door?
- Answer: First door has Voldemart, and the second has Harry (Solve using truth tables)
(b) You enter another secret hall and encounter two more closet doors. This time, Snape says that either both doors are true or both doors are false.
i. First Door: Harry is behind at least one of these doors.
ii. Second Door: Voldemort is behind the other door.
Who is behind each door?
- Answer: Same - First door has Voldemart, and the second has Harry (Solve using truth tables)
Attendance Kabir, Vansh, Kushagra, Rohan, Shikher, Rehaan, SidharthM, Vivaan, Rhea, Advay, Aashvi, Mihir, Aneesh, Aarkin, Arjun
Class puzzles (repeat from class 53)
Homework:
Introduce Euler/Venn diagrams (For purpose of this lesson, we are not differentiating between the two)
- Items are members of sets. Example: Humans is a set of which you and me are members
- Overlapping sets imply that items inside that overlap are members of both
- Draw Venn diagrams for two sets A and B, if nothing else is known about them
- Establish correspondence to truth table of two statements, each being T or F
- Draw Venn diagram for "All humans are mortals" - correspondence with truth table
- If "Socrates is human", then what must it mean about his mortality?
- What is A or B, A and B, not A in Venn diagrams?
- What is A implies B in Venn diagrams? (Technically, it should be worded as "a is member of A implies, a is member of B")
- Draw possible Venn diagrams for " No A is B . Some C is A. " What can we say about C and B?
- Three cases - C and B can be disjoint, C can include all of B, or C can include part of B.
- Repeat the Venn diagram formulation of other examples above
Exercises
- Let kids draw conclusions, and draw truth tables and venn diagrams for the following
- Some cats have no tails, All cats are mammals. What can we say about mammals having tails?
- Some mammals have no tails
- All horses have hooves; No humans have hooves. What can we say about humans being horses?
- No humans are horses
- Mistakes in deduction
- Some A are B; some B are C; what can we say about A being C?
- Some cats are black things; some black things are televisions. What can we say about cats being televisions?
- All A are B; All A are C; what can we say about relationship between B and C
- All cats are feline; all cats are mammals. What can we say about mammals being feline?
- No A is B; No B is C; What can we say about relationship between A and C?
- No fish are dogs; No dogs can fly. What can we say about fish being able to fly?
Some fun with venn diagrams
- Draw a giant venn diagram with two sets "Have a sibling", "Have a dog". And let students write their names on relevant portions. (In an in-person class, draw these circles on the floor and let students stand on relevant portions)
- Draw a venn diagram of four languages, and ask all students to place themselves in the right section. Ask students to draw conclusions from this sample. Are these conclusions relevant to all of humanity?
- There are sandwiches at the canteen, and 44 different students want different condiments:
- 11 wanted ketchup and relish
- 8 wanted mustard and relish
- 28 wanted ketchup
- 6 wanted ketchup, relish and mustard
- 20 wanted mustard
- 14 wanted relish
- 10 wanted ketchup and mustard
Draw a venn diagram to illustrate these choices
A 5-set Venn diagrem
.png)
Homework:
- Dudeney - 381: Can you construct a card frame, one as shown below, so that each side adds up to the same number
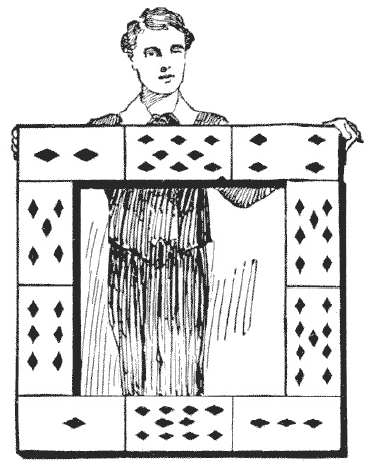
- Answer:
.jpg)
References:
Math Circles for Elementary School Students, By Natasha Rozhkovskaya (Online Google)
https://ia902701.us.archive.org/4/items/AmusementsInMathematicspdf/AmusementsInMathematics.pdf - Dudeney